目录
- 1、cpu 流水线带宽限制
- 2、port 或者说 cpu 执行单元的限制
- 3、内存的相关指令限制
- 4、内存和缓存带宽限制
- 5、循环上下文依赖限制
- 6、前端处理限制
- 7、每周期的分支指令限制
- 8、乱序执行窗口的大小限制
- 补充:
最近在对项目中的代码做性能测试,性能优化其实很枯燥,基本是按照一些固定的原则慢慢一步一步照着做就好了。例如一些常见的原则:
选择合理的数据结构 尽量使用标准库函数,避免自己实现相同逻辑 尽量少做字符串拼接,如果要,尽量使用带缓冲区的接口 尽量使用标准库排序,少使用自定义排序 尽量使用局部变量 尽量延迟加载 尽量使用缓存
在用工具一点一点分析的时候,突然心中产生一个疑问:到底优化到什么时候是个尽头?也就是到底什么时候我该停下来?什么时候代码的执行才达到了极限呢?
正好最近看到一篇针对 cpu 性能优化的文章写的很有意思:Performance Speed Limits
文章忽略了 cpu 做分支预测的逻辑,正好之前我也写过 cpu 分支预测做代码优化的内容,可以在这里查看:关注 cpu 的执行做代码优化
这次看到的文章把别的方面又讨论了一下,分析了若干种影响代码运行速度的限制,有意思的地方在于作者对于影响代码执行速度的考虑角度,从这些角度可以帮助我们理解 cpu 是怎么执行代码的,文章很长,我只挑拣出我感兴趣的部分记录一下:
作者详细分析了到底是哪些因素影响了代码的执行速度,为了说清楚这个问题,作者拿循环来做分析跟举例说明,这样更容易理解。当然这里作者只讨论纯粹的 cpu 执行代码的角度,而不考虑代码质量跟实际作用的角度,单纯看影响 cpu 执行代码性能的因素有哪些。
1、cpu 流水线带宽限制 #
现代 cpu 架构一般都是超标量流水线式架构,能够在一个 cpu 周期内,同时取多条指令分发给不同 cpu 执行单元来执行,比如整数、浮点计算、加载、存储可以并行执行,所以每个 cpu 周期能够执行多条指令已经是标配,但是能够执行的指令依然是有上限的,这个上限在不同的 cpu 架构,cpu 指令集下各不相同。这个流水线带宽即是指一个 cpu 周期能够执行的指令数量的限制,来看个例子:
uint32_t top = 0, bottom = 0;
for (size_t i = 0; i < len; i += 2) {
uint32_t elem;
elem = data[i];
top += elem >> 16;
bottom += elem & 0xFFFF;
elem = data[i + 1];
top += elem >> 16;
bottom += elem & 0xFFFF;
}
比如这段代码编译成汇编指令如下:
top:
mov r8d,DWORD [rdi+rcx*4] ; 1
mov edx,DWORD [rdi+rcx*4+0x4] ; 2
add rcx,0x2 ; 3
mov r11d,r8d ; 4
movzx r8d,r8w ; 5
mov r9d,edx ; 6
shr r11d,0x10 ; 7
movzx edx,dx ; 8
shr r9d,0x10 ; 9
add edx,r8d ; 10
add r9d,r11d ; 11
add eax,edx ; 12
add r10d,r9d ; 13
cmp rcx,rsi ; (fuses w/ jb)
jb top ; 14
右边的数字写明了是第几条指令,比较特殊的是 cmp 跟 jb 两个指令是可以融合成一条指令执行的,所以最后是 14 条。
Intel 的 Skylake 架构 cpu 同一个周期可以执行 4 条指令,所以理论上,上面这个循环每一次迭代需要耗费 14 / 4 = 3.5 个周期,每次循环处理了两个元素,所以每个元素实际消耗的 cpu 周期是 1.75 个,这个就是从理论上能够得到的执行上限了,比如 data 数组有 100 个元素,那么就需要 1.75 * 100 = 175 个 cpu 周期,再计算单核 cpu 的执行频率,就能够算出极限需要多少时间才能完成循环。
2、port 或者说 cpu 执行单元的限制 #
上面第一点算出的执行上限其实在绝大部分情况下是无法达到的,因为我们完全忽视了具体的指令是什么,而 cpu 的执行单元是有限个数的,比如做浮点数运算的 FPU 一周期能够执行的浮点数运算指令就是有限的。所以你不可能在一个周期内执行太多条需要占用 cpu 相同执行单元的指令,这个也很好理解。 举个例子:
uint32_t mul_by(const uint32_t *data, size_t len, uint32_t m) {
uint32_t sum = 0;
for (size_t i = 0; i < len - 1; i++) {
uint32_t x = data[i], y = data[i + 1];
sum += x * y * m * i * i;
}
return sum;
}
编译成汇编算一下指令数:
.top:
mov r10d,DWORD [rdi+rcx*4+0x4] ; 1 y = data[i + 1]
mov r8d,r10d ; 2 setup up r8d to hold result of multiplies
imul r8d,ecx ; 3 i * y
imul r8d,edx ; 4 ↑ * m
imul r8d,ecx ; 5 ↑ * i
add rcx,0x1 ; 6 i++
imul r8d,r9d ; 7 ↑ * x
mov r9d,r10d ; 8 stash y for next iteration
add eax,r8d ; 9 sum += ...
cmp rcx,rsi ; i < len (fuses with jne)
jne .top ; 10
比较特别的是 data[i] 和 data[i+1] 被编译器聪明的合并成了一条取数据指令,因为上一次循环里取到的 data[i+1] 正好是下一次循环的 data[i]。cmp 跟 jne 也是一样融合成一条指令,所以最终一次循环的指令数是 10 条。计算一下 10 / 4 = 2.5 个周期。但事实上运行上述代码会发现实际上一次循环需要 4 个周期。为什么会这样呢?限制在于 imul 指令。imul 是乘法指令,但这条指令一个周期只能执行一条,所以它成为了瓶颈,每次循环有 4 条 imul 指令,导致每次循环都需要至少 4 个周期才能执行完。
在 cpu 上,所有指令是通过投递到不同的 port 来执行的,这些 port 其实就对应到不同的执行单元,如图:

imul 指令会始终投递到 p1 这个 port 来执行,关于不同的汇编指令会投递到哪个 cpu 的 port 可以在这里查到。
一些简单的整数计算(add、sub、inc、dec),按位运算(or、and、xor)和一些标志位测试(test、cmp)可以在多个 port 上投递,所以这些指令一般不会成为瓶颈,但也有很多指令是竞争相同的 port 来执行的,例如位移指令跟位测试指令 bt\btr 就共用 p1 和 p6 端口,popcnt 跟 tzcnt 就只在 p1 端口上执行等等。
3、内存的相关指令限制 #
(主要指吞吐量限制:加载、存储、访问总限制、复杂寻址限制)
对于 cpu 来说在一个周期内,加载、存储、访问地址的指令数量是有限制的。
加载吞吐量限制 #
我们假设所有需要访问的数据都在 L1 级缓存当中,则常见的 cpu 都会有 2,3 个加载指令的限制。这个限制其实跟第 2 点 port 的限制相同,但是它又有特别的地方,所以单独拿出来说。
比如代码:
do {
sum1 += data[offsets[i - 1]];
sum2 += data[offsets[i - 2]];
i -= 2;
} while (i);
编译后:
; total fused uops
.top: ; ↓
mov r8d,DWORD PTR [rsi+rdx*4-0x4] ; 1
add ecx,DWORD PTR [rdi+r8*4] ; 2
mov r8d,DWORD PTR [rsi+rdx*4-0x8] ; 3
add eax,DWORD PTR [rdi+r8*4] ; 4
sub rdx,0x2 ; (fuses w/ jne)
jne .top ; 5
它有 5 条指令,所以理论上来讲需要 5 / 4 = 1.25 个周期,实际上需要 2 个周期,因为它有 4 条 load 指令,而我们的 cpu 每个周期最多执行 2 条加载指令,需要 2 个周期。
加载分割高速缓存行的情况 #
从 L1 级缓存加载数据的指令计数为 1 次指令,但如果 load 指令触发了高速缓存行的分割,那么消耗就要翻倍。分割高速缓存行的频率取决于加载数据量的大小,在 intel 平台上,对于 N 字节的数据,需要按照 (N - 1) / 64 的概率来分割缓存行。
规避措施 #
一般来说加载成为瓶颈的情况不常见,但是如果真的成为瓶颈了,一种解决途径是进行批量加载,这里的批量不是指数据的大小,而是指加载的次数。比如上面那个例子,对于 data 的两次加载是随机的,没办法批量处理,但是对 offsets 的两次加载却是可以合批的,可以把这两个 32 位数据的访问合并成一个 64 位的访问:
do {
uint64_t twooffsets;
std::memcpy(&twooffsets, offsets + i - 2, sizeof(uint64_t));
sum1 += data[twooffsets >> 32];
sum2 += data[twooffsets & 0xFFFFFFFF];
i -= 2;
} while (i);
编译之后是:
.top: ; total fused uops
mov rcx,QWORD PTR [rsi+rdx*4-0x8] ; 1
mov r9,rcx ; 2
mov ecx,ecx ; 3
shr r9,0x20 ; 4
add eax,DWORD PTR [rdi+rcx*4] ; 5
add r8d,DWORD PTR [rdi+r9*4] ; 6
sub rdx,0x2 ; (fuses w/ jne)
jne .top ; 7
把 2 次 offset 的 load 减少到 1 次,这样就用 alu 的计算操作来换取了 load 的次数,现在这个版本的指令书有 7 个,比之前的版本多了 2 条指令,但实测下来运行周期却只有 1.81 个周期,比之前 5 条指令需要 2 个周期要快。
存储吞吐量限制 #
跟加载类似,存储指令也有数量限制,通常一个周期可以执行 1 条或者 2 条存储指令。
存储分割高速缓存行的情况 #
比如在 intel cpu 上,超过 64 位的存储都会算错至少两条存储指令。
总的访问限制 #
上面单独讨论了加载跟存储的访问限制,实际上在常见 cpu 上,他们的总数也会有一个组合限制。一般来说是小于单独的限制之和的。例如,AMD Zen 3 cpu 上每个周期都可以执行 3 次加载,或者 2 次存储,但总共只有 3 个地址生成单元,所以总的限制是加载、存储最多 3 次。
复杂寻址限制 #
跟上面谈到的总访问限制类似,对于 cpu 来说 AGU 也就是地址生成单元的个数是有限的,比如 intel 的 Skylake 芯片上通常有 3 个,对应的端口是 p2、p3 和 p7。正常来说上面的总的访问限制就是 3,但 p7 这个 port 本身是有限制的,它只能被 store 指令使用,并且只有在 store 是简单寻址的情况下才可以用。 当然,自 Ice Lake 架构以来,这个限制也没有用了,因为加载跟存储分别都单独的 AGU 了。
规避措施 #
这种规避方式也比较简单,就是尽量让循环中的寻址方式改成简单寻址,用指针移动的方式代替索引比如:
mov [rdi + rax*4], rdx
add rax, 1
改成
mov [rdi], rdx
add rdi, 4
当然这也是说起来容易做起来难的事。比如下面的例子把两个数组的元素写入第三个数组:
void sum(const int *a, const int *b, int *d, size_t len) {
for (size_t i = 0; i < len; i++) {
d[i] = a[i] + b[i];
}
}
编译成如下:
.L3:
mov r8d, DWORD PTR [rsi+rax*4]
add r8d, DWORD PTR [rdi+rax*4]
mov DWORD PTR [rdx+rax*4], r8d
add rax, 1
cmp rcx, rax
jne .L3
这个循环有 5 条指令,本来只需要 5 / 4 = 1.25 个周期,但受到复杂寻址的限制影响,需要花费 1.5 个周期,因为有一个存储指令使用了复杂寻址,然后再加上一个加载指令。如果我们给每个数组使用单独的指针做简单寻址如下:
.L3:
mov r8d, DWORD PTR [rsi]
add r8d, DWORD PTR [rdi]
mov DWORD PTR [rdx], r8d
add rsi, 4
add rdi, 4
add rdx, 4
cmp rcx, rdx
jne .L3
都使用了简单寻址,但是却多加了两条指令,因此需要 7 / 4 = 1.75 个周期,反而更慢了。但其实我们还可以再修改一下,仅对存储指令使用指针,如下:
.L3:
mov eax, DWORD PTR [rdx+rsi] ; rsi and rdi have been adjusted so that
add eax, DWORD PTR [rdx+rdi] ; rsi+rdx points to a and rdi+rdx to b
mov DWORD PTR [rdx], eax
add rdx, 4
cmp rcx, rdx
ja .L3
这样就依然是 5 条指令,而且减少了复杂寻址。当然在使用高级语言的时候,你很难一开始就想出来该怎么编码,比如上面的汇编逻辑变成代码如下:
void sum2(const int *a, const int *b, int *d, size_t len) {
int *end = d + len;
ptrdiff_t a_offset = (a - d);
ptrdiff_t b_offset = (b - d);
for (; d < end; d++) {
*d = *(d + a_offset) + *(d + b_offset);
}
}
4、内存和缓存带宽限制 #
上面关于加载和存储的吞吐量限制都做了一个前提假设,就是所有的访问都命中了 L1 级缓存。但其实所有级别的缓存都有格子的带宽限制。离 cpu 越远的缓存在一个周期内能够访问的平均缓存行数就越小。内存的带宽限制就更复杂一点,不过通常来说你很难在一个 cpu 周期内达到 DRAM 的带宽限制,因为很难产生能填满总线的请求。这里列举一下常见的 cpu 以及不同级别一个周期能访问的缓存行限制:
| Vendor | Microarchitecture | L2 | L3 (Shared) |
|---|---|---|---|
| Intel | CNL | 0.75 | 0.2 - 0.3 |
| Intel | SKX | 1 | ~0.1 (?) |
| Intel | SKL | 1 | 0.2 - 0.3 |
| Intel | HSW | 0.5 | 0.2 - 0.3 |
| AMD | Zen | 0.5 | 0.5 |
| AMD | Zen 2 | 0.5 | 0.5 |
| AMD | Zen 3 | 0.5 | 0.5 |
5、循环上下文依赖限制 #
即最长依赖链中的延迟总和
到目前为止讨论的都是吞吐量的硬限制,就是 cpu 每个周期内只能做到这么多事。还没有考虑每条指令本身执行就需要花费时间,在实际情况中,这却是很重要的。比如考虑一下上面的乘法循环的修改版本:
for (size_t i = 0; i < len; i++) {
uint32_t x = data[i];
product *= x;
}
每次迭代仅执行一次乘法操作,编译如下:
.top:
imul eax,DWORD PTR [rdi]
add rdi,0x4
cmp rdi,rdx
jne .top
只有 3 条指令,根据前面的逻辑 3 / 4 = 0.75 个周期就能执行完。但我们知道 imul 指令需要 p1 这个 port 来执行,另外两条指令可以在别的 port 上执行,因此由于 p1 的限制,我们猜测需要 1 个完整的周期才行,实际情况呢?
$ ./uarch-bench.sh --timer=perf --test-name=cpp/mul-chain --extra-events=uops_dispatched_port.port_0#p0,uops_dispatched_port.port_1#p1,uops_dispatched_port.port_2#p2,uops_dispatched_port.port_3#p3,uops_dispatched_port.port_4#p4,uops_dispatched_port.port_5#p5,uops_dispatched_port.port_6#p6
Benchmark Cycles p0 p1 p2 p3 p4 p5 p6
Chained multiplications 2.98 0.48 1.00 0.50 0.50 0.00 0.52 1.00
花费了 2.98 个周期来执行这 3 条指令。 为什么会这样呢?可以看到 imul 指令有 3 个周期的延迟,这意味着只有在执行开始后 3 个周期后才能获得结果,这跟之前的预测大相径庭。这是因为在每次迭代中,乘法的结果都取决于前一次循环的乘法结果,因此乘法指令只能在前一次循环完成的时候才能开始,即 3 个周期后。所以 3 个周期就是每次循环的时间限制。
我们关心的是循环携带的依赖关系,也就是一次循环中某些输出的寄存器在下一次循环作为了输入。在更早的例子中,4 个 imul 指令形成了一条更复杂的依赖链:
.top:
mov r10d,DWORD [rdi+rcx*4+0x4] ; load
mov r8d,r10d ;
imul r8d,ecx ; imul1
imul r8d,edx ; imul2
imul r8d,ecx ; imul3
add rcx,0x1 ;
imul r8d,r9d ; imul4
mov r9d,r10d ;
add eax,r8d ; add
cmp rcx,rsi ;
jne .top ;
注意每一个 imul 指令是如何依赖前一条指令的输出寄存器 r8d 的,并把最终结果放入 eax 寄存器中,然后 eax 寄存器又作为了下一次循环的输入。所以我们的循环间依赖其实只是由于 eax 的依赖导致的:
iteration 1 load -> imul1 -> imul2 -> imul3 -> imul4 -> add
|
v
iteration 2 load -> imul1 -> imul2 -> imul3 -> imul4 -> add
|
v
iteration 3 load -> imul1 -> imul2 -> imul3 -> imul4 -> add
|
v
etc ... ...
可以看到虽然 imul 指令并没有直接参与依赖,但由于 eax 寄存器的依赖关系,导致 imul 指令也进入了依赖链。事实上上面我们所有的例子都存在这样的依赖链,但因为它相对于前面讨论的限制足够小,并没有成为瓶颈,所以在前面都忽略了。当存在多个依赖链时,我们的执行速度限制就取决于最长的依赖链的执行时间了。
意外的地方 #
你会发现前面讨论的时候因为依赖链的存在,应该需要 3 个周期才能完成一次循环,但实际我们测试的数据是 2.98 个周期,为什么我们测试的结果会比理论值还要小,是不是哪里出错了,是测量精度的误差吗? 其实不然,这是由于测试的结构导致的,测试代码有 4096 个元素的数组,因此会有 4096 次循环。而调用测试例子本身执行了 1000 次,每次调用执行 4096 次循环。而在内部循环的每次调用之间,乘法链其实是可以重叠执行,每个链长度为 4096 个元素,每次函数开头都会启动一个新的乘法链:
uint32_t mul_chain(const uint32_t *data, size_t len, uint32_t m) {
uint32_t product = 1;
for (size_t i = 0; i < len; i++) {
// ...
因此,在每个循环末尾的附近可能会有少量重叠的情况出现,这是由于 cpu 的无序指令缓存导致的。
补救措施 #
针对依赖的措施也就是打破依赖关系了。例如可以使用较低延迟的指令(如加法位移等)来代替乘法。一种更普遍的做法是用多个并行的依赖来代替一个长链依赖。在上面的例子中,乘法的结合性允许我们用任何顺序来进行乘法。比如,我们可以在每次循环中,用多个乘积来并行做乘法,然后在最后再把它们相乘,如下:
uint32_t p1 = 1, p2 = 1, p3 = 1, p4 = 1;
for (size_t i = 0; i < len; i += 4) {
p1 *= data[i + 0];
p2 *= data[i + 1];
p3 *= data[i + 2];
p4 *= data[i + 3];
}
uint32_t product = p1 * p2 * p3 * p4;
现在理论上只需要 1 个周期就可以执行完一次循环,依赖链导致的延迟被消除了。但实际上每次循环至少需要 3 个周期,因为现在 imul 指令的并发成为了新的限制,因为 imul 指令只能运行在 p1 端口上,所以形成了新的限制。
6、前端处理限制 #
(主要指微指令解码器和 uop 缓存处理的数量限制)
在以前,微指令的缓存跟解码器本身也会带来限制,它的速度本身可能影响代码的执行速度。比如传统的解码器 MITE 每个周期最多只能处理 16 字节的指令,因此如果指令的平均长度超过 4 个字节,那么一个周期最多也就只能执行少于 4 条指令了。而且一个周期能够访问的 uop 缓存条目也是有限制的,假如一个周期只能访问一个 uop 缓存条目,而一个条目只包含例如 6 条指令,那么一个周期也就只能最多执行 6 条执行了。当然现在新的 cpu 架构已经很大程度的降低了前端解码器的限制。
7、每周期的分支指令限制 #
这一点就更 track 了,例如 intel 限制了每 2 个周期最多能执行 1 个分支指令。如果在循环中存在更多更大的分支,那么这个限制也会限制代码的执行速度。
8、乱序执行窗口的大小限制 #
cpu 为了并发执行更多的指令,会对代码的执行顺序进行调整,也就是所谓的乱序执行。但是很少有人会考虑到 cpu 对于指令乱序的处理会收到乱序窗口大小的限制,导致 cpu 并非能够一口气把循环体内的所有指令都完美的处理成可以并发执行的乱序指令流。 我们前面的所有讨论,都默认了 cpu 存在一个无限大小的乱序指令窗口。这也是为什么我们在讨论依赖链时说只有循环携带的依赖才是重要的,隐含的假设是说我们有无限的能力来重排这些指令,让他们可以完美的乱序执行,所以在非依赖的执行链中我们直接认为所有的指令都可以完美的并发执行。但真实的 cpu 中,这个乱序的能力是有上限的。如果每次循环有 1000 条指令,而无序窗口只有 100 条指令,那 cpu 就无法完美的让所有可以并行执行的指令都重叠的并发执行,那些相距较远的指令就无法重叠执行。 当然,乱序窗口可不止一个大小限制,列举一下所有乱序窗口类的大小限制在下面:
| Vendor | Microarch | ROB Size | Sched (RS) | Load Buffer | Store Buffer | Integer PRF | Vector PRF | Branches | Calls |
|---|---|---|---|---|---|---|---|---|---|
| Intel | Sandy Bridge | 168 | 54 | 64 | 36 | 160 | 144 | 48 | 15 |
| Intel | Ivy Bridge | 168 | 54 | 64 | 36 | 160 | 144 | 48 | 15 |
| Intel | Haswell | 192 | 60 | 72 | 42 | 168 | 168 | 48 | 14 |
| Intel | Broadwell | 192 | 64 | 72 | 42 | 168 | 168 | 48 | 14 |
| Intel | Skylake | 224 | 97 | 72 | 56 | 180 | 168 | 48 | 14? |
| Intel | Sunny Cove | 352 | 160 | 128 | 72 | 280 | 224 | ? | ? |
| AMD | Zen | 192 | 180 | 72 | 44 | 168 | 160 | ? | ? |
| AMD | Zen 2 | 224 | 188 | 72 | 48 | 180 | 160 | ? | ? |
| AMD | Zen 3 | 256 | >192 | 72 | 64 | 192 | ? | ? | ? |
| Apple | M1 Firestorm | 636 | 326 | 130 | 60 | ~380 | ~434 | ~144 | ? |
| Apple | M1 Icestorm | 111 | 71 | 30 | 18 | ~79 | ~87 | ? | ? |
| Amazon | Graviton 2 | ~124 | ~48 | ~62 | ~40 | ~92 | ~96 | ~46 | ? |
重排缓冲区大小 #
ROB 是最大且最通用的乱序缓冲区,所有微指令都会在 ROB 中占用一个槽。该结构保存着从分配开始到退出为止的指令,所以它对完整的乱序窗口设置了严格的上限。例如,load 指令如果未命中高速缓冲,那么在数据被加载到之前,load 指令都无法退出 ROB,假设 load 指令需要 300 个周期才能完成,那么它将一直在 ROB 中存在这么长时间。
加载缓冲区大小 #
每个加载操作都需要一个加载缓冲区,加载缓冲区就存在上表中的限制。一般常见的加载缓冲区是 ROB 的 1/3 大小。因为如果超过 1/3 的操作都是加载,那么就有可能触碰到这个加载缓冲区大小的限制。
存储缓冲区大小 #
跟加载缓冲区类似,每个存储操作都需要一个存储缓冲区。而存储缓冲区被填满几乎是存储指令产生性能问题的唯一方式。跟加载不同的是存储指令几乎没有人会等待其完成,除非做存储转加载的操作。存储缓冲区通常小于加载缓冲,大概是加载缓冲的 2/3 的大小,这也反映了一个事实就是大部分程序的加载需求都多余存储需求。
调度程序缓冲区大小 #
发出指令操作后,它会停留在调度缓冲区中直到能够被执行。它通常比 ROB 小的多。在现代 cpu 上通常有 40-90 个指令大小。如果有太多指令依赖尚未完成的较早指令时,就有可能触碰到这个限制。例如一个未命中的加载指令之后,有大量的指令依赖该加载,在完成加载之前,这些指令都会堆积在调度缓冲区中。
寄存器文件大小限制 #
在 cpu 中用来记录寄存器地址跟数据的告诉缓冲也是有大小限制的,它是寄存器的集合。只有当指令退出时寄存器才会被回收。但实际中一些指令并不会消耗寄存器文件,比如分支指令之类的。
运行中的分支顺序缓冲区 #
这里的分支指的是在运行中尚未退出的分支数量,是指条件跳转和间接跳转例如 jcc where cc 或者 jmp [rax] 这类指令产生的分支。一般很少会达到它的限制。
运行中的调用缓冲区 #
其实就是指运行中的 call 指令的数量限制。一般是 14-15 个在 intel cpu 上。一般来说减少 call 的调用,或者用内联来替换。
补充: #
这里推荐一个非常好用的工具 llvm-mca,使用 -timeline 编译选项可以直接查看指令的执行时序图,使用 -bottleneck-analysis 编译选项还可以帮忙分析出执行瓶颈所在,用 -dispatch 指令还可以设置流水线宽度,-iterations 可以指定执行次数。
如果不想用命令行工具可以直接在 compiler explorer上使用这个工具,相当不错。
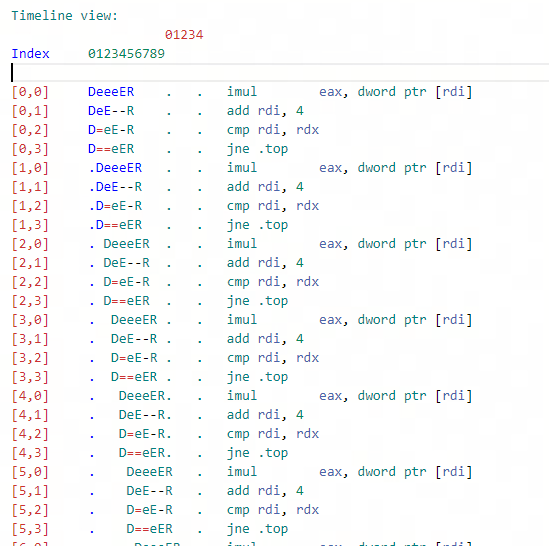
每个字母的具体含义可以看这里

如果看完我的摘要还想查看原文的可以再去作者的文章里看一下 Performance Speed Limits