关注 cpu 的执行做代码优化

June 16th, 2021

比较有意思的是最近这段时间，连续看了好几个针对 cpu 做性能优化的分析。其中关于二分查找的优化比较有代表性，这里做个记录，免得忘了。

首先是月初在知乎看到一篇关于 Rust 的 binary_search 优化的文章： https://zhuanlan.zhihu.com/p/371460665

文章详细描述了作者关于如何把 Rust 标准库里的 binary_search 最优时间复杂度从 O(log n) 优化到 O(1) 的。我就只提取相关内容来说。这个优化说来也挺简单，就是之前 Rust 的二分搜索里有相同元素时，会一直查到最后一个返回，所以是 O(log n) ，现在改成每次循环先判断是否跟目标相等，如果相等就立马返回，于是最优时间复杂度就变成 O(1) 了。

while size > 1 {
    let half = size / 2;
    let mid = base + half;
    // SAFETY:
    // mid is always in [0, size), that means mid is >= 0 and < size.
    // mid >= 0: by definition
    // mid < size: mid = size / 2 + size / 4 + size / 8 ...
    let cmp = f(unsafe { s.get_unchecked(mid) });
    if cmp == Equal {
        return Ok(base);
    } else if cmp == Less {
        base = mid
    };
    size -= half;
}

有意思的地方出现了，理论上，改动之后的版本应该在任何情况下都会比之前的要快才对，然而事实是这种改动只有在重复元素较多的情况下才会比普通的情况性能要好。这是为什么呢？

先说结论。熟悉cpu指令集流水线的朋友可能已经猜到了。这位程序员添加的这个 if 判断导致了 cpu 的分支预测失败，结果花了大量的时间在清空流水线的回滚操作上。这里涉及了一个概念就是 cpu 分支预测，具体内容可以看 wiki ： https://en.wikipedia.org/wiki/Branch_predictor

简单的说就是现代处理器，为了更快速的执行指令，在遇到分支的时候会主动做出预测，根据以往的执行经验，提前把预测分支的指令加载并执行掉，如果预测成功就毫无停顿，如果预测失败，就需要清空指令流水线从预测失败的地方重新开始加载指令，这个清空回滚的操作在出现大量预测失败的情况时是非常耗时的，比如就像这里的 for 循环里添加了一个判断是否找到目标，找到就返回的分支。

为了避免 cpu 的分支预测失败，对于那些大部分情况下判断失效的分支就应该尽量避免在循环逻辑中出现，什么意思呢？就比如这个程序员在二分查找的 for 循环里添加的这个 if 判断，判断的是是否查找到目标元素，而在 for 循环的过程中，这个分支判断成功只可能有一次，其他没有找到的情况全部分支预测失败，所以 cpu 在循环过程中不停的回滚指令流水线导致性能下降。

无独有偶，前几天在刷云风的一篇关于优化二分查找算法的文章： https://blog.codingnow.com/2021/06/binary_search_by_guess.html

文章内容波澜不惊，但是在评论里发现了一个词： eytzinger order 。于是就去搜了一下，发现了一篇雄文： https://algorithmica.org/en/eytzinger

文章很长，我简单的总结一下，就是普通的有序数组，在做二分搜索的时候对 cpu 的缓存并不是非常友好，为什么呢？因为在搜索的过程中，这个有序数组的每个位置的元素被访问的概率是不同的，每个二分段中间的元素被访问的概率更高，有下面这个图的关系：

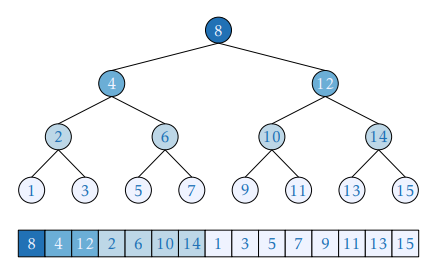
比如这样一个 1-15 的有序数组，在二分查找的过程中，8 被访问的概率最高，其次是 4 跟 12，依次往下。这个也很好理解，仔细想一下二分搜索的过程就会发现每一个 for 循环开始都是先找二分的位置，然后继续二分下去。

所以，如果 1-15 的内存布局是按照常见的有序数组那样存放，是不利于 cpu 做缓存预取操作的。这里又涉及到一个概念， cpu 的缓存预取。

简单说来，cpu 的缓存比内存要快太多，所以 cpu 要加载数据的时候一般是按照缓存级别一级一级的查找，如果找不到才从内存加载，一般 cpu 从内存加载数据也不会是一个一个的，而是一块一块的加载进缓存，这样缓存的作用才能被最大利用到。为什么可以这么做呢？基于两个基本事实，就是我们的程序在数据访问模式上有两个特点，一个是时间局部性，也就是在短时间内很有可能会反复访问同一块数据；另一个空间局部性，也就是访问一个位置的数据后，很可能会立马访问其周围位置的数据。所以 cpu 从内存加载整块的数据进缓存是一个不错的加速策略。

由此分析，在二分搜索的时候，如果能把有序数组按照上面那样的访问频率来安排数组的内存布局会更有利于 cpu 的缓存预取策略。上面那样的布局就被称为 eytzinger order。当然这需要一些额外的处理跟接口调用，不是重点。

真是大开眼界。顺便欣赏一下这样处理之后的二分搜索代码，看得我虎躯一震。同样你会发现这个程序员也考虑了上面提到的 cpu 分支预测的情况，在 for 循环里没有提前判出。

#pragma GCC optimize("O3")
#include <bits/stdc++.h>

using namespace std;

const int n = (1<<20);
const int block_size = 16; // = 64 / 4 = cache_line_size / sizeof(int)
alignas(64) int a[n], b[n+1];

int eytzinger(int i = 0, int k = 1) {
    if (k <= n) {
        i = eytzinger(i, 2 * k);
        b[k] = a[i++];
        i = eytzinger(i, 2 * k + 1);
    }
    return i;
}

int search(int x) {
    int k = 1;
    while (k <= n) {
        __builtin_prefetch(b + k * block_size);
        k = 2 * k + (b[k] < x);
    }
    k >>= __builtin_ffs(~k);
    return k;
}

不知道是不是巧合，优秀的程序员都在二分搜索这个算法问题上关于 cpu 的处理做了一段精彩的阐释。

以前我在考虑代码性能的时候，更多的是从算法的角度，时间复杂度的角度去思考一段代码的执行效率。很少从 cpu 执行的角度去考虑性能的问题，这次也算是打开了眼界，这可能也是理论到实践之间的细微差别，这样思考问题更加实事求是脚踏实地。

Comments

programmer (22)