起念：有趣的问题

起因是上周六晚上，朋友在群里问了一个有意思的问题：

玩一个游戏，一个人在 1-100 之间想一个数字，然后你来猜，猜错了会告诉是大了还是小了，如果 1 次猜中给 5 美元，2 次给 4 美元，3 次给 3 美元，4 次给 2 美元，5 次猜中给 1 美元，6 次 0 美元，7 次倒贴 1 美元，8 次倒贴 2 美元，9 次倒贴 3 美元。问你应该玩吗？

作为程序员的第一反应其实很朴质，这不是明显的二分查找吗？100 小于 $2^7$ 次方， 7 次以内必然能猜中。所以并不存在 8，9 次以及之后的情况。只需要考虑 7 次内猜中的数学期望即可。

思考每次猜完得知大小后，缩小范围继续二分的猜测就可以了。以 [1, 100] 为例，第一次猜个 50，如果高了，就把上限改成 49，从 1 - 49 中二分猜测，低了就改为从 51 - 100 中二分，然后一直缩小，最终一定能在 7 次以内猜中。

计算一下概率，假设 P(n) 为 n 次猜中的概率，那么 P(1) = 1/100 毫无争议，P(2) 呢？
按照二分的策略，每次能够缩小一半的猜测空间，所以 P(2) 应该等于第一次猜不中的概率，乘以第二次缩小空间后猜中的概率：

第一次猜不中有两种情况：
如果第一次猜大了，则范围缩小为 1 - 49，第二次猜中的概率就是 1/49
如果第一次猜小了，则范围缩小为 51 - 100，第二次猜中的概率是 1/50

第一次猜大了的概率是多少呢？因为我们第一次猜的是 50，如果出题人所想的数字满足均匀分布的话，比 50 小的概率就是 [1, 49] / 100 = 49/100，而比 50 大的概率是 [51, 100] / 100 = 50/100，和猜中的概率 1/100 合在一起正好等于 1。

所以 P(2) = 49/100 * 1/49 + 50/100 * 1/50 = 2/100，依照类似的方式计算

P(3) = 4/100

P(4) = 8/100

P(5) = 16/100

P(6) = 32/100

P(7)无法继续二分了，所以概率是 1 - sum(P(1-6)) = 37/100。

于是可以算出来期望的钱为：E = P(1) * 5 + P(2) * 4 + P(3) * 3 + P(4) * 2 + P(5) * 1 + P(6) * 0 + P(7) * -1 = 0.2。

换一个角度验证一下，比如我们以纵坐标表示能够获得的美元，横坐标表示一开始所想的数字，采用二分的策略进行游戏，画出对应的图，再对 1 - 100 获得的美元求和即可得到 20 美元，因为对 1 - 100 求和，所以是进行了 100 次游戏，所以单次游戏的期望是 0.2，跟上面概率计算的结果一致。

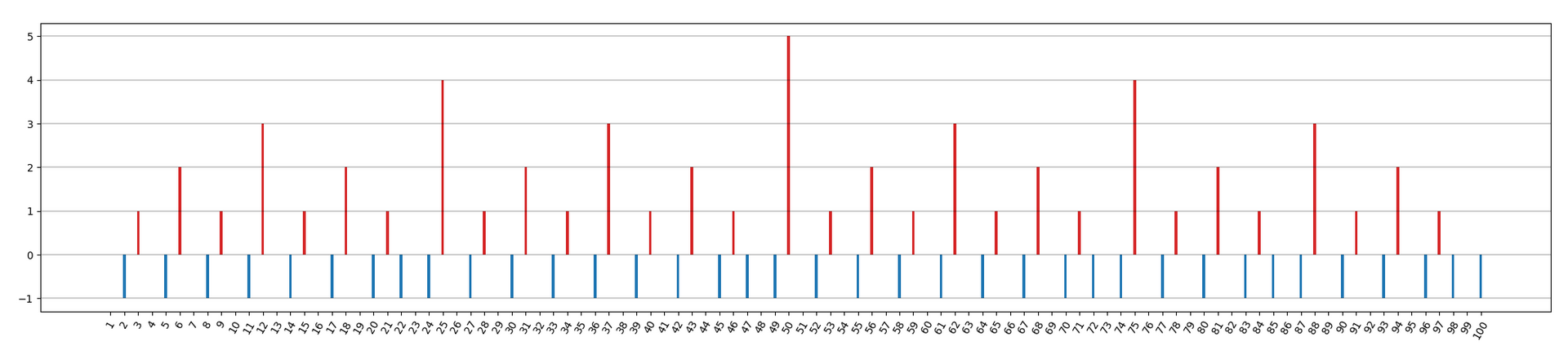
验证：写段代码试试

可是口说无凭，在群里跟朋友解释了半天也没用，最后一怒之下，决定写一段代码验证一下：

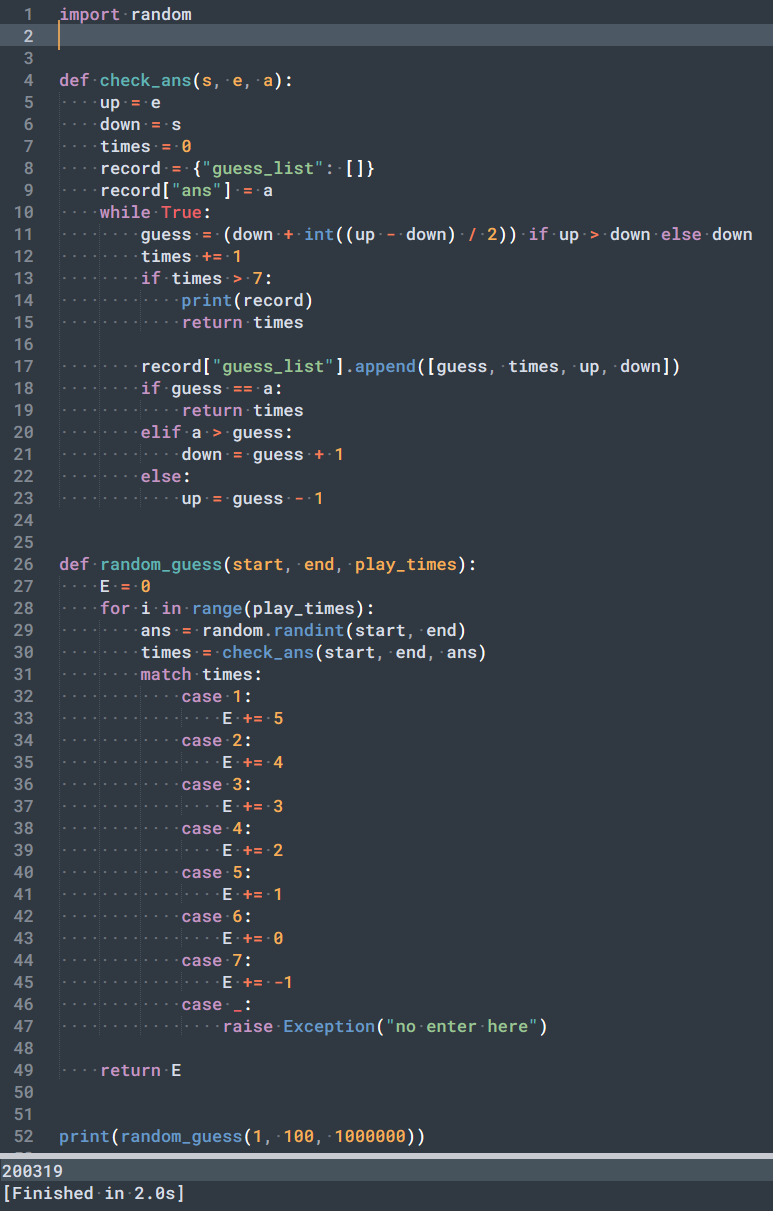
代码逻辑其实就是模拟上面猜测的过程调整上下界，然后做二分，为了说服朋友不会出现超过 7 次的情况，还特意加了异常跟结果打印。随意跑个 100w 次，结果也跟预期的期望一致，至此终于说服了朋友。

更进一步：应对作弊

睡在床上还在翻来覆去想这个问题，突然一个想法进入大脑：如果这个跟你玩的人已经考虑到你会采取二分的策略，而他偏偏就每次都选那些会让猜 7 次的数字怎么办？还要跟他玩这个游戏吗？比如他每次都选数字 100，那么显然采取这样的策略会导致你每次都输 1 美元。

于是我想到了另一个策略，就是只需要首次猜测随机选择一个数字，而不是严格的选 50 进行二分，就可以很完美的规避对手的固定策略，当然这也会导致猜测次数不再是永远至多 7 次，而来到了需要至多 8 次。这也很好理解，因为第一次切分没有完美的切分成 49 或者 50 两个范围，导致可能出现第一次切分导致一边超过 $2^6$ = 64 个，于是这一边的猜测就需要 7 次，再加上最开始的一次，一共就是 8 次。这样期望会发生变化，由于 8 次会扣除 2 块钱，所以出现 8 次最大猜测次数的时候期望会跳变一下。而 8 次的期望可以大致估算一下，明显是负数。为了维持住猜测次数在 7 次以内必然结束的期望，那么第一次切分除了不严格二分以外，还需要保证切分出来的两部分都必须在 $2^6$ 以内，这样后续二分才可以在 6 次结束，于是第一次切分的随机范围便可以在 [37, 64] 之间，这样就可以保证不会存在任何一部分超过 $2^6$ - 1。总体依旧保持 7 次必然结束的期望。

更进一步思考，在 [37, 64] 之间选择初始切分点，会对整体的期望有影响吗？

可以想到这里的期望将不再是一个固定值，而是随着第一次猜测的等分程度来确定的，第一次猜测越靠近中点，期望值越接近完美的期望 0.2，于是又爬起来写了个程序验证了一下，验证的过程也很简单，就构造一下首次选择不同切分点，剩下做二分的逻辑保存一下结果即可：

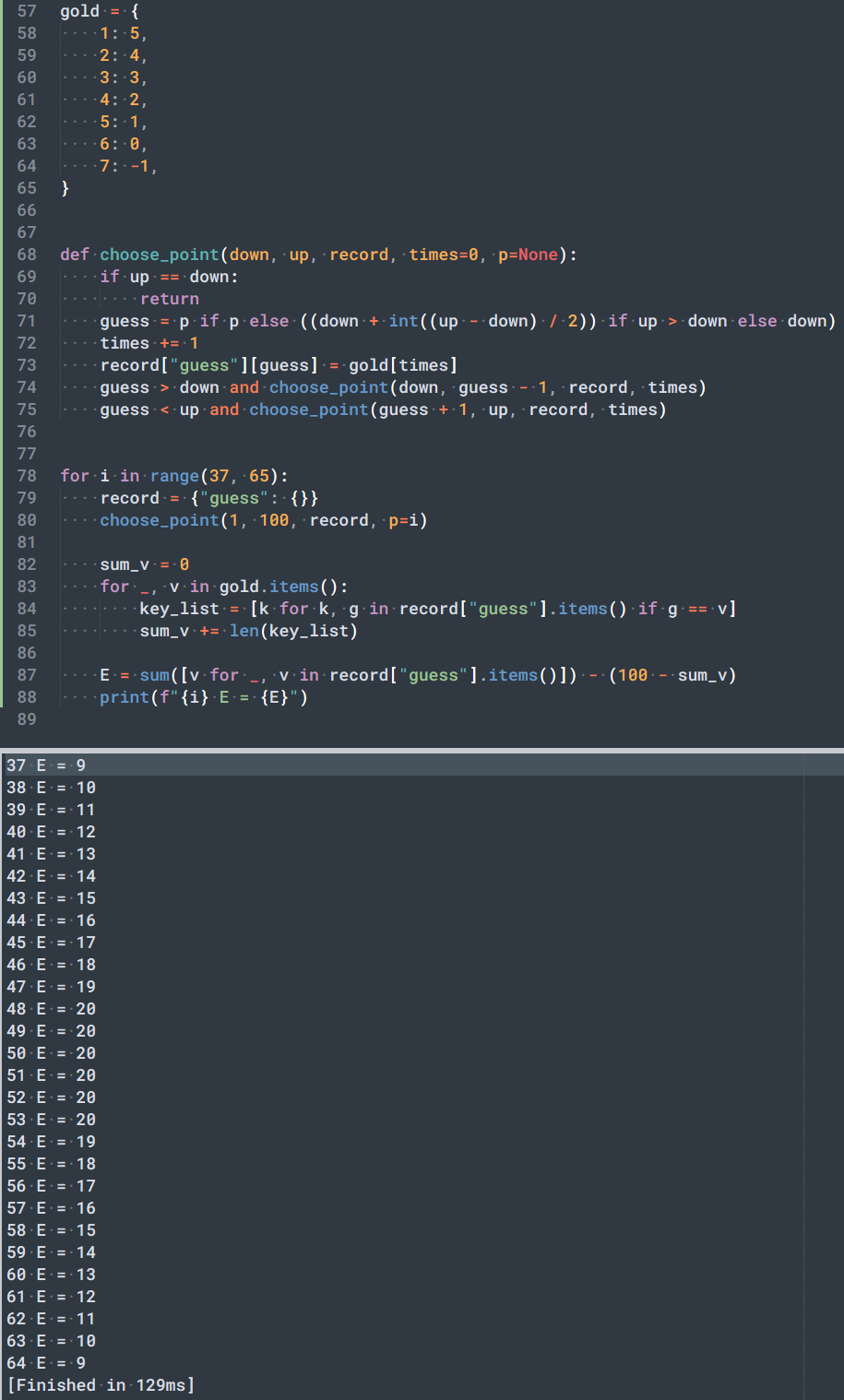
可以明显看到，当切分点更靠近 50 完美切分点附近时，期望越接近最大值 20，而偏离中心点越远，期望会逐渐减少。这也符合我的预期。可以安心睡觉了。

解释：信息熵？

第二天醒过来，脑子里还在想这个问题，思考二分的本质到底是什么？该如何解释这种选择呢？

其实可以从信息论的角度理解，因为出题人会告诉我们每次猜测是大了还是小了，这样会帮助我们缩小猜测范围，相当于告诉了我们信息，那么我们选择猜测哪个数得到的信息量就不是均等的，它能够每次帮助我们筛选掉更多数字的那些猜测带来的信息量更大。在信息论中，计算信息量的公式是  $-log_2 P$，P 是事件发生的概率，在我们的游戏中，假设我们一开始猜测 50，然后出题人告诉我们猜小了，这意味着结果一定在 [51, 100] 中，所以我们瞬间得到了这个数字在原先 100 个数中的 50 个数字当中，筛选掉了一半的数字，得到了 50/100 概率的信息，也就是  $-log_2 (50/100)$ 的信息量，而如果告诉我们比 50 要小，那么就得到了 $-log_2 (49/100)$ 的信息量；而如果 50 正好命中，这个概率是 1/100，所以我们得到的信息量最大即 $-log_2 (1/100)$，这也是显然的，因为我们一次就猜中了当然信息量是最大的。

那么我们要判断哪个数字作为我们的首选，也就是需要选择那个能带来最大信息量的数字，可以想到用事件发生的概率乘以它带来的信息量，也就是 $\sum$(P * $-log_2 P$)，其实这个就是信息熵的定义。
那么选择 50 做首次切分的信息熵即是：
50/100 * ($-log_2 (50/100)$) + 49/100 * ($-log_2 (49/100)$) + 1/100 * ($-log_2 (1/100)$) $\approx$ 1.07072

不如计算一下初始选择所有数字的信息熵这样更能够清晰的看到是不是二分是最佳策略:

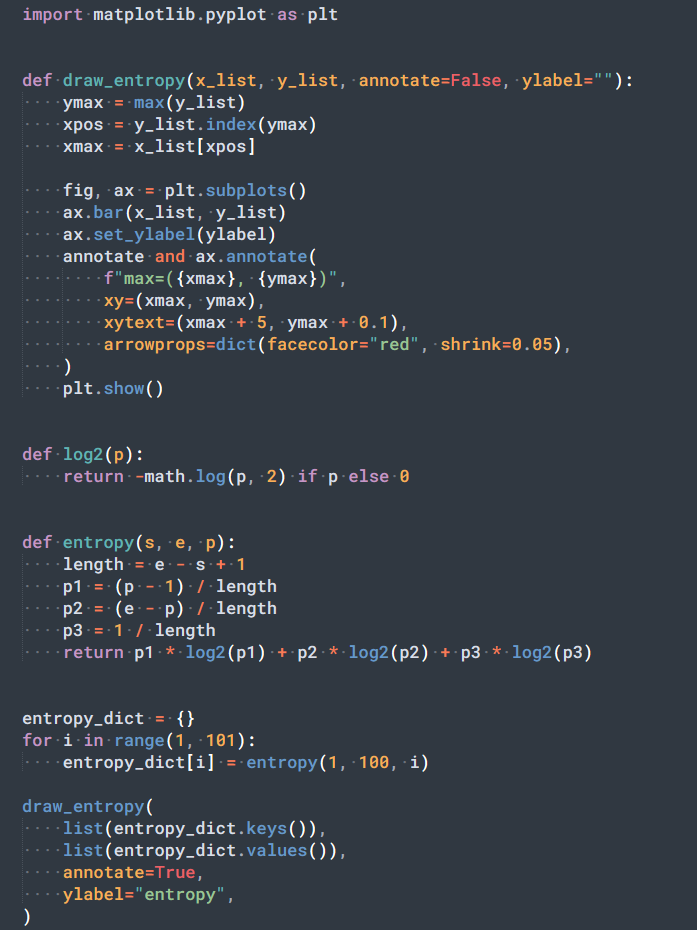
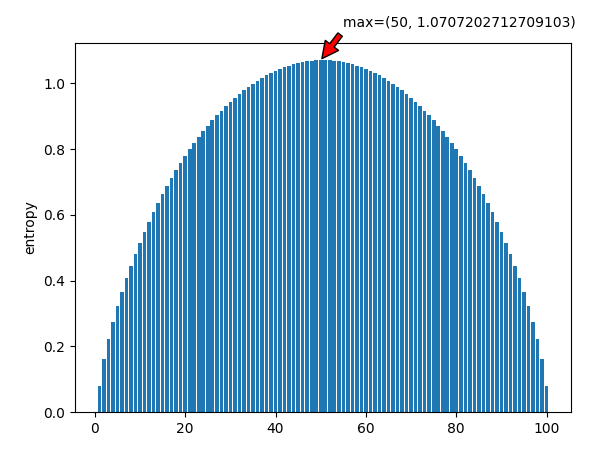
可以看到二分确实是信息熵最大的选择。

尾声

后来好奇，在群里问了一下为什么朋友突然想到这么个奇怪的问题，他告诉我原来是他前几天在油管看到一个采访关于如何通过面试的，微软前 CEO 史蒂夫·鲍尔默在采访中提出了这个问题：How to Pass an Interview, According to Ex-Microsoft CEO Steve Ballmer

鲍尔默在采访中说他如果被问到这个问题，肯定是不会玩的，因为他觉得期望是负的。然后朋友觉得期望不一定是负数，所以有此一问。

这么看微软 CEO 也不怎么样嘛 :)，也许我比他当的好呢。