SLG 常见需求
上周我的小伙伴碰到一个问题无法解决,于是跑过来问我。
问题是这样的:我们的策划想要在玩家进入游戏的时候在地图上给他随机找一个地块放下主城。但是要求这个地块不能被其他游戏内的要素占据了位置,比如不能跟其他主城重叠,不能跟地图上的建筑重叠等等。
这是一个 SLG 游戏的常见需求,说白了就是给玩家随机一个地方落下主城。但是我的小伙伴左思右想,似乎没有找到一个比较合理的算法来处理它。

因为我们的地图是按照矩形格子进行切分的,地图上的所有要素也都是若干个矩形方格组成。所以咋看一下这个问题,可以抽象成在一个矩形区域内,已经挖去了若干个矩形的洞,如何在剩下的面积中均匀的随机放置我请求放下的新矩形。
均匀随机
先抛开这个问题,思考一下更加简单一般的情况。
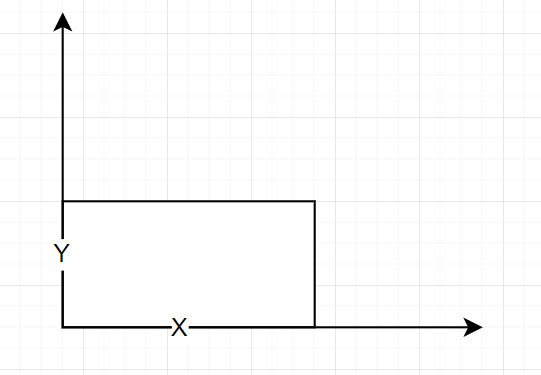
比如如何在一个矩形区域内均匀随机一个位置。这个很容易就能想到,因为在矩形中,想要确定一个位置只有两个维度,随机一个 X 和 Y 的坐标就可以完全确定一个矩形内的位置。而 X 和 Y 是两个正交的坐标轴,所以可以分别均匀随机就好。
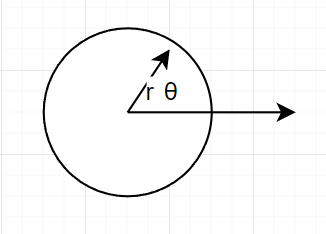
如果不是矩形区域呢,比如是一个圆形区域。这个也很容易处理,因为对于圆形区域,只需要采用极坐标系,就可以发现,随机一个半径长度,再随机一个绕圆心旋转的角度,就可以得到圆内的任意一点。这种方式也是比较常见的做法。
那么如果在矩形区域内挖去了一个洞,如何在剩下的面积上做均匀随机呢?
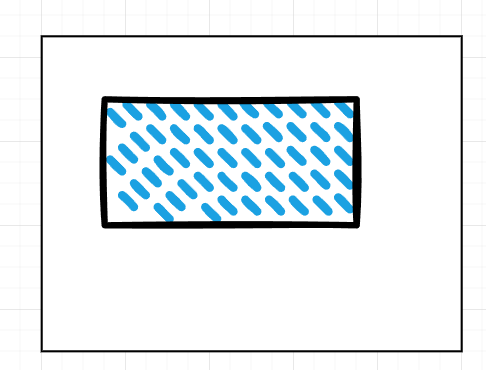
抓住面积这个本质
我们先来分析一下,所谓的均匀随机,其实就是在这样的一个面积内闭着眼睛撒豆子,然后睁开眼看豆子落在哪就是哪,思考一下这个过程,其实就是按照面积进行随机,比如我把一个矩形从中线一分为二,那么豆子落在这两个小矩形上的概率就都是 50%。
所以,如果一个矩形中被挖去一部分,那么我们只需要用剩下的面积来撒豆子就行了。
于是一个最朴质的算法就诞生了,就是闭着眼睛撒豆子,再睁开眼,如果豆子落在了不是洞的位置,就记录下来当作随机结果,如果豆子落在了洞里,就重新撒一次,直到豆子落在非洞区域。
这个算法还是很容易用代码写出来的:
do {
x = rand(w)
y = rand(h)
} while ((x, y) in holes)
但这个算法有个弊端,就是如果矩形区域内的大部分面积都被洞覆盖了的情况下,这个循环预计会进行很多次之后才能跳出来。也就是在糟糕的情况下,这个算法将足够糟糕。作为程序员对这样的算法怕是不能忍受的。不过小伙伴一开始也是这样写的,因为是内网,没有多少玩家跟地图要素的情况下工作的也挺好。
切分面积
小伙伴跟我说了这个问题之后,我思考了一下,经过几天的努力终于写出了一个合理的算法。
再重新看看上面那个有洞的矩形,既然我们的目标是要在矩形的剩下面积中均匀随机出一个位置,再结合我上面想到的把矩形一分为二之后豆子落在每个小矩形上的概率是均等的想法,一个新的算法呼之欲出了。
我只需要把被洞挖去的矩形切割开来,把它分成不同的小矩形,然后统计每块矩形的面积相加之后,在总面积上进行随机,然后看随机结果落在哪个切分的小矩形上,之后再在这个小矩形面积上进行均匀随机 X 和 Y,就可以得到一个新算法,在挖洞矩形剩余面积上的均匀随机算法。
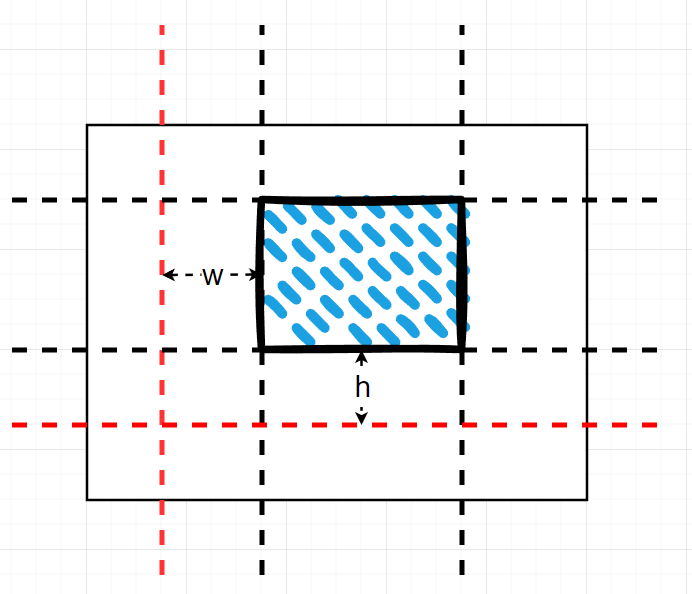
拿上面的图举例子:
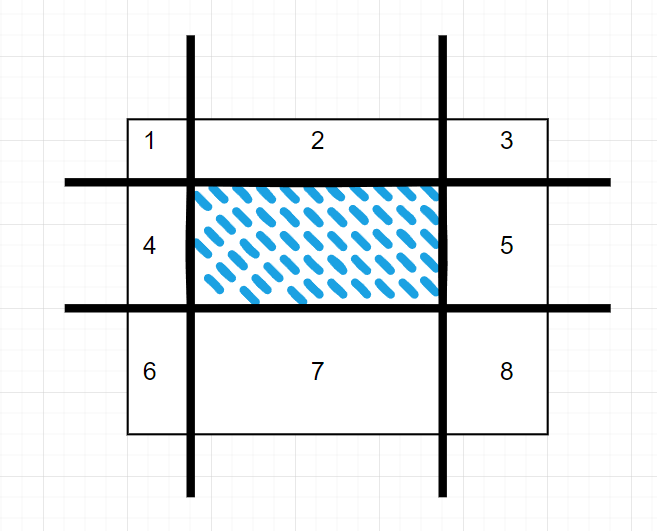
比如我可以按照矩形洞的四边,把整个大矩形切割成 8 个小矩形块。然后计算每个小矩形块的面积 $ S_1,S_2… S_8 $,再把所有小矩形块的面积加起来 $ S_{total} = \sum_{i=1}^{8}S_i $。
接着只需要 $ rand(S_{total}) $ 看落在哪一块面积上,再对那块矩形随机一个 X 和 Y,就能够求出一个精确的位置满足均匀随机的条件。
这个逻辑写出来也很容易:
/* split rectangle according to all holes */
/* sum all area */
target = rand(all_area)
for (i = 0; i < count_area; i++) {
if (target <= area[i]) {
x = rand(area[i].w)
y = rand(area[i].h)
return x, y
}
}
这个算法的关键,在于需要把被洞挖掉之后的矩形,用若干小矩形进行拼接,构成剩余的空洞矩形,一个朴质的切割方式,就是按照每个洞的边进行切分,这样一定能保证完成这样的矩形切割。
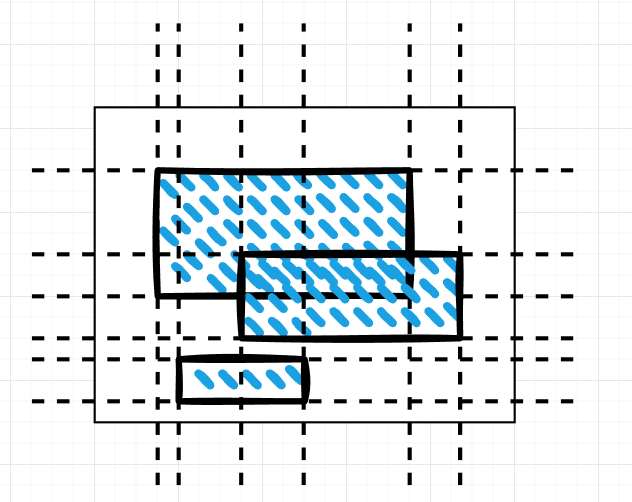
切割完之后,只需要判断每个小矩形是否在洞内,去掉在洞内的矩形之后剩下的就都是合法的区域了。至此,这个算法也算实现完了。
可以看到每个洞都会给 X 和 Y 方向增加 2 条切割线,所以最终每个方向的切割线数量是洞的数量的 2 倍,最终切割出来的面积就是洞的数量的平方的 4 倍。所以从算法的角度看,这个算法的时间复杂度是 $ O(n^2) $ ,n 是洞的数量。一个 $ n^2 $ 的算法,在实际使用中已经足够了,没有太多优化的必要。
新的需求
就在我以为一切都 ok 的时候。又有了新的变化。原来策划要求的并不仅仅是随机出一个点,而是要随机的放下一个矩形。因为随机出一个位置后要把玩家的主城给放进去,如果这个位置太靠近任何一个洞或者地图边缘就无法放进这个矩形了。
这下问题要复杂一些了,因为之前的切割方案没有考虑到随机出的位置必须要满足一定的条件才行。而这个条件就是能够放下一个指定大小的矩形。本来我觉得这应该是一个比较常见的需求,于是在网上找了一下, 居然没有找到一个现成的算法。只好自己继续思考了。
上面想到的算法在整体思路上没有太大问题,现在的问题是如何把“能否放下想放的矩形”这个限制条件考虑进去。
在纸上画了一下,发现如果想在地图上塞进一个 w * h 大小的矩形,真正不能放的地方,就是那些洞的边缘,如果能找到一种办法过滤掉这些洞边缘的区域,就又回归到上面的算法中来了。再进一步思考,终于让我找到了办法。
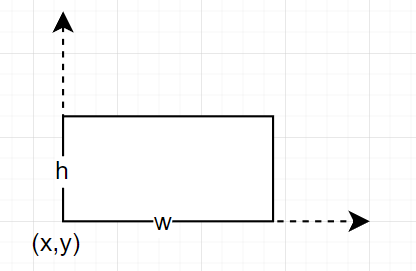
因为要随机一个位置放下一个矩形,所以我先约定如何表达一个矩形。常规的想法是四个点表示一个矩形,但从数学上看只需要两个点,左下角跟右上角就够了。为了更加方便写代码,我用左下角的点加上矩形的宽、高,这样一个四元数来表达一个矩形(x,y,w,h),这样约定后,只需要找到一个合法的左下角的点,就找到了对应的矩形。
接着来考察哪些区域能够合法的塞下左下角的点就会发现,在每一个洞矩形的左边 - w 跟下边 - h,也就是洞矩形的 (x - w)、(y - h) 处,这两根线之内靠近洞的部分是无法放入这个新矩形的。
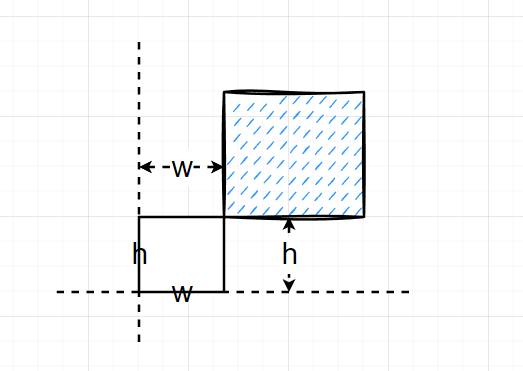
于是一个很自然的想法就形成了,只需要在每个洞的左边左偏 w 距离切一刀,下边偏下 h 处再切一刀,这样就把不符合条件的面积切去了。这个新的切割方法应运而生。
当然,在实现的时候还是有很多细节的。
首先,切割线并不是简单的把原本洞的左侧跟下侧单纯外拓了,洞本身的左侧跟下侧切割线依然需要保留,因为边界条件下,会出现允许在一条边甚至一个点上进行随机。
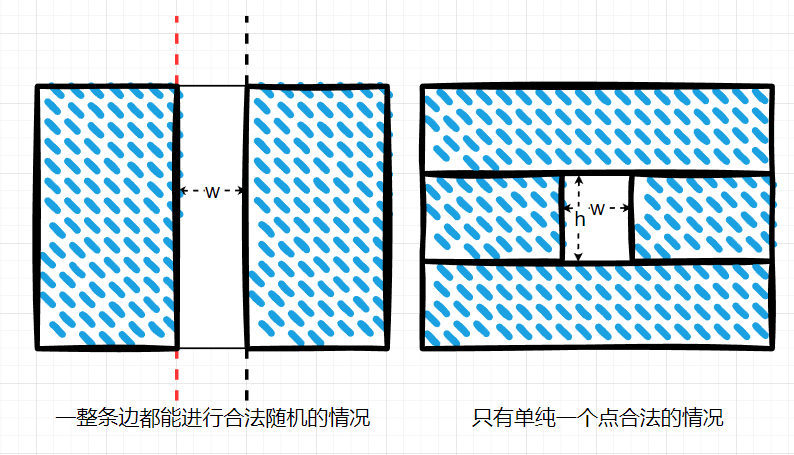
所以原始洞的边切割线依然需要保留,在对整个矩形进行切割之后,需要筛选出哪些切割出来的部分是整个面积都可以进行随机的,哪些区域是只有一条边可以进行随机的,哪些区域是单纯只有一个点可以的。当然,对于点和边的区域还要考虑到是否有必要跟其他区域进行合并,如果这条合法的边或者点属于另外一个合法区域,那么这条边和点就可以从最终的所有合法区域中去掉,因为重复计算了。
其次,就是为了保证是均匀随机,对于一条边跟一个点是没有面积的概念的,所以怎么把单独的边跟点也统计进最终的总面积里呢?这里有个小技巧,就是我们真正在随机的其实并非是数学上意义上的任意位置,而是一个坐标为整数的位置,那么一个点的坐标位置就是 1,一条边的整数位置是边长 + 1,而一块面积的整数点位是 (边长 + 1) * (边长 + 1),所以我们很天然的能够计算出所有合法的面积区域、边区域、点区域的合法位置总和,然后进行随机就好。随机到面积区域就再随机一个 X、Y 坐标,随机到一个边区域就再随机一个边长,随机到一个点区域就直接是那个点。
由于切割之后对每个区域需要检查是否在洞的外拓大区域内,所以这个算法的时间复杂度是洞数量的三次方,这是一个 $ O(n^3) $ 的算法。这就不太高效了,可以预估一下在当前普通 CPU 上,当洞的数量达到 $ 10^3 $ 这个数量级的时候,算法计算出随机位置的结果应该就会超过几百毫秒了。
我实现了一版这个效果,不做任何代码优化的情况下,洞数量在 800 左右,计算一个随机结果大致在 100 ms 左右。代码放在了 github 上 https://github.com/rangercyh/randplace,有需要的朋友可以看看, 也希望有人一起帮忙优化一下,或者有别的更好的方式也欢迎留言讨论。