August 16th, 2022

这两天看了篇文章 Fast random shuffling 很有意思。

写的内容主要分析了一下大名鼎鼎的随机打乱算法 Fisher-Yates shuffle 在具体使用代码实现当中的性能开销。

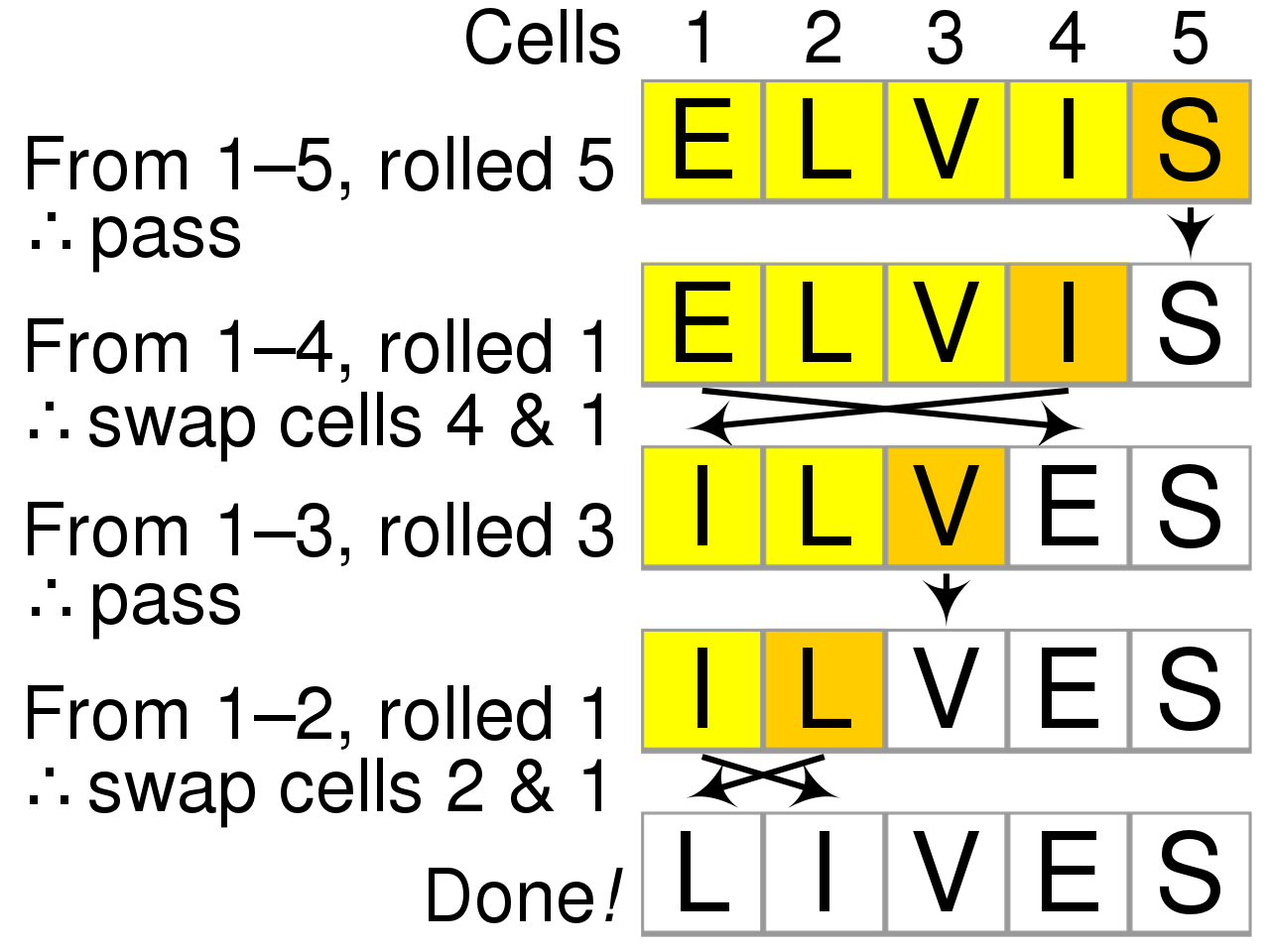
比如一段典型的实现代码如下：

for (i=size; i>1; i--) {
    int p = random_bounded(i); // number in [0,i)
    swap(array+i-1, array+p); // swap the values at i-1 and p
}

在不考虑使用类似 SIMD 之类的 CPU 并行指令集以及不考虑 CPU 缓存方式的情况下，对于上述代码，单纯从实现原理上进行分析。可以看出，除了每轮循环的读写变量之外，最耗时的，必然是那个随机算法。

这个随机算法需要生成一个在指定范围内的整数。一直以来，经典的计算机实现方式都会用到除法操作。比如 Go 在实现随机库 rand.go 里的代码：

func (r *Rand) Int31n(n int32) int32 {
    if n <= 0 {
        panic("invalid argument to Int31n")
    }
    if n&(n-1) == 0 { // n is power of two, can mask
        return r.Int31() & (n - 1)
    }
    max := int32((1 << 31) - 1 - (1<<31)%uint32(n))
    v := r.Int31()
    for v > max {
        v = r.Int31()
    }
    return v % n
}

这段代码里显然用到了两次除法（取模即是除法）。在 Java 语言、PCG 这样的专业随机库里、以及其他一些随机的实现里，这样的函数都至少包含一次除法。

可惜的是除法是一个很重的操作，比其他的运算符都要重很多倍。

那么如何消除除法呢？

伪随机步骤：

首先让我们理解一下为什么这里需要除法。

这个问题很容易理解。因为对于计算机来说，做伪随机有两个步骤。

第一个步骤，绝大部分的随机做法都是先通过各种方法生成一个 32 bit 或者 64 bit 或者更长位数的随机串；

第二个步骤，通过取模操作来把这个串映射到你所需要的随机范围内，以此来达到在指定范围内的随机。

关于第一个步骤各家有各家的想法，有的人想用物理真随机来生成这样的串，比如有用地球大气参数模拟真随机的 Random.org，还有用破坏量子态相干来做真随机的高速量子随机数发生器，但目前大部分的随机库采集的真随机源还是比较常见的计算机内部的物理扰动带来的随机噪声，比如 Openssl 的随机库就需要计算开机运行一段时间才能采集足够的噪声来产生可靠的真随机源。在此我们不讨论生成真随机串的步骤。

第二个步骤才是需要除法的关键，因为所求的范围通常比想要的随机位数少，32 bit 的随机串，能够表示的范围是 $[0,2^{32})$，假设我们需要在 $[0,s)$ 内等概率随机一个值。那么一个常见的做法是用 $[0,2^{32})$ 上的真随机值去对 s 取模求余数。

当然，这种做法存在一个显然的问题。这并不是一个真正等概率的随机结果。举个简单的例子。

我们真随机得到 $[0, 2^{3})$ 这 8 个数字，现在想获得 $[0,3)$ 上的等概率随机。我们可以看到取模之后的结果如下：

0	1	2	3	4	5	6	7
% 3 =
0	1	2	0	1	2	0	1

我们希望得到 0, 1, 2 的概率各是 1/3 ，实际上我们得到 0, 1, 2 的概率分别是 3/8, 3/8, 2/8。

在所求范围远小于真随机范围的情况下，这样的取模操作会非常接近等概率随机，但依然不是真正的等概率。而在所求范围非常接近真随机范围的情况下，这个误差会更大。我们可以很容易得出一个误差范围，能够发现对于 $[0,2^{32})$ ，用这种取模的映射方法会使得对于 $[0,N)$ 的每一个数出现的次数范围在 $[floor(2^{32}/N),ceil(2^{32}/N)]$ 内。

所以这里碰到两个问题：

取模需要用到除法，除法操作是很费 CPU 时间的；
取模之后的结果并非是等概率随机。

问题一

取模：

先来看第一个问题，取模操作会包含一个除法指令。而除法比乘法要耗时的多。一个 32bit 的除法操作，在最近的 x64 的处理器上，依然需要 6 个 CPU 周期才能执行一条并且存在 26 个周期的延迟，相对的乘法操作却只需要 1 个 CPU 周期以及 3 个周期的延迟。

当然，在现代编译器下，如果在编译期已经确定了被除数的大小，那么会有一系列针对它的优化，比如把除法转变成若干个乘法和一些其他指令。

但我们还可以做得更好，直接从算法层面优化它。这就是这篇文章的核心观点。

化除为乘

仔细想想，为什么会需要取模？

原因是想把一个 32bit 数映射到一个更小的数值范围。让我们假设我们的真随机数是一个 32bit 的数 x，然后我们所求的范围应该是一个小于 $2^{32}$ 的数 N。有什么办法可以找到一个更加高效的映射呢？

文章作者想到了一个绝妙的映射，就是计算 x * N，然后除以 $2^{32}$，这样就可以得到一个在 $[0,N)$ 上跟取模类似概率的映射。

uint32_t reduce(uint32_t x, uint32_t N) {
    return ((uint64_t) x * (uint64_t) N) >> 32 ;
}

把一个原本耗时的除法转变成了一个乘法和一个位移操作。这样就把平均耗时降低到接近 2 个 CPU 周期，并且缩小到了 4 个周期的延时。

作者做了一下测试，发现有大约 4 倍的性能提升，想了解细节的朋友可以看看作者的代码 fastrange.c，CPU 周期对比：

modulo reduction	fast range
8.1	2.2

Amazing !!!

跟取模一样吗？

现在回头看看这个算法在 $[0,N)$ 上的概率。

通过把 $[0,2^{32})$ 真随机数乘以 N，我们相当于把 $[0,N)$ 映射到了 $[0,N * 2 ^ {32})$，然后通过除以 $2^{32}$，又把 $[0,2^{32})$ 内的数全部映射成 0，$[2^{32},2 * 2^{32})$ 内的数全部映射成 1，依此类推。接下来我们只需要看每个 $2^{32}$ 的间隔区间内，N 的倍数出现的概率是否相等就可以。

我们假设 N 恰好可以整除 $2^{32}$ 。这显然使得每个区间中的 N 的倍数最大化，事实上每个 $2^{32}$ 区间内，我们都可以找到 $ceil(2^{32} / N)$ 个 N 的倍数。而如果 N 无法整除 $2^{32}$，存在余数，那么对于每个 $2^{32}$ 区间都会存在一个额外的余数子区间。最坏情况下，一个区间我们只能得到 $floor(2^{32} / N)$ 个 N 的倍数。由此可以看出，这跟我们上面取模的操作是类似概率的。

更精确分析一下，能够发现当第一个完整 N 区间出现在 $2^{32}$ 区间的最开始处，N 的倍数的数量是最大化的，$2^{32}$ 区间的最后会有一个不完整的 N 区间；而如果 N 的第一个完整区间出现在 $2^{32} mod N$ 处，那么最后就不会存在一个不完整的 N 区间。这意味着只要 N 的完整区间出现在 $2^{32} mod N$ 之前，在这个 $2^{32}$ 区间内就会有 $ceil(2^{32} / N)$ 个 N 的倍数，否则我们只有 $floor(2^{32} / N)$ 个。

依然拿上面的例子来看，比如我们能够生成 $[0,2^3)$ 区间内的随机数，现在要求生成 $[0,3)$ 的随机数。我们用 $2^3 * 3$ 得到一个最长的数轴，接着我们按照 $2^3$ 对数轴进行切割，然后计算每个切割区间内的 3 的倍数的个数。

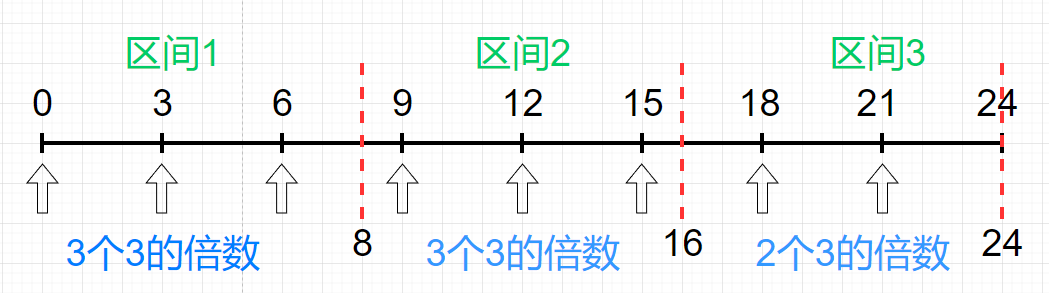
可以看出，对于每一个长度为 $2^3 = 8$ 的区间，如果第一个完整的长度为 3 的区间在 $2^3 mod 3 = 2$ 之前，比如区间 1 跟区间 2，那么这个区间就会有 $ceil(2^3 / 3) = 3$ 个 3 的倍数，否则比如区间 3 就只有 $floor(2^3 / 3) = 2$ 个 3 的倍数。

能够知道哪个区间会出现 $ceil(2^{32} / N)$ 哪个区间会出现 $floor(2^{32} / N)$ 吗？假设我们有一个在 $[0,2^{32})$ 内的随机数 k，我们只需要找到第一个不小于 $k2^{32}$ 的 N 的倍数的位置就好了。于是我们只需要用 $ceil(k2^{32} / N)N - k2^{32}$ 和 $2^{32} mod N$进行对比，如果前者比后者小，那么这个区间的值就是 $ceil(2^{32} / N)$ 否则就是 $floor(2^{32} / N)$。

由此终于把一个除法运算解决掉了。之后在进行随机的时候就可以用以下代码代替取模操作了：

uint32_t random_bounded(uint32_t range) {
    uint64_t random32bit =  random32(); //32-bit random number 
    multiresult = random32bit * range;
    return multiresult >> 32;
}

问题二

到此，问题一圆满解决。关于问题二，随机的概率并非是等概率该如何解决呢？

首先得明确，问题二并不像想象中那么严重，因为对于理想中的真随机在计算机中无法实现。我们一直以来假设的前提条件，计算机可以产生一个 32bit 的真随机数其实是一个伪命题。所以在这样一个伪随机的情况下去追求真实等概率没有太大意义。不过作为程序员，我们依然应该怀有美好的愿望来写代码，否则一切将变得太过无聊。

现在把问题抽象一下，在解决掉问题一之后，有了一个高效的在 $[0, N)$ 上的非等概率随机发生器，现在如何得到一个 $[0,N)$ 上的等概率随机发生器呢？

这其实是一个很有意思的问题。在 Stackoverflow 上有一个类似的问题。问的是有一个 $[0,1]$ 的非等概率随机器，其中 0 的出现概率是 p，1 的出现概率是 1 - p，那么如何用它来实现一个 0、1 出现概率均是 1/2 的随机器。

实现的代码很简单：

int UnbiasedRandom()
{
    int x, y;
    do
    {
        x = BiasedRandom();
        y = BiasedRandom();
    } while (x == y);
    return x;
}

就是连续随机两次，去掉两次结果相同的那些过程，如果结果不同，就取第一个随机结果。

为什么这段代码可以呢？

因为成对事件 p(1-p) 和 (1-p)p 发生的概率是相同的，换句话说就是 01 串跟 10 串出现的概率是相等的。所以只要连续随机两次，如果发现两次结果是 01 串或者 10 串，就取第一个数字就好了，如果是 00 或者 11 串，直接抛弃就好，因为我们不知道 pp 跟 (1-p)(1-p) 是不是相等的。

好神奇的解法。

冯·诺依曼出场

就在我感叹解法神奇的时候，发现二楼给出了这个解法的出处。

没想到在我不长的计算机生涯中，第一次跟传说中的大神 冯·诺依曼 有了联系。原来这个解法在他的一篇小记中出现过 Paper: Various Techniques Used in Connection With Random Digits，这种解法可以叫拒绝采样，应该在统计学中比较常用。

对于上面这 2 种概率的情况，出现成对等概率事件 01 和 10 的概率 $z = 2 * p * (1-p)$，而预期的执行次数期望是 $1/z$。举例来说，如果出现 0 的概率是 $p = 0.99$ 的话，算出来将需要调用 50 次才能出现想要的 01 或者 10 串。初看上去这个算法还行，再考虑到它是大神出品的，所以大胆猜测它是一个最优算法。但很可惜，它不是（原来大神也有翻车的时候 ;D）。

根据香农极限我们可以发现，在这种情况下，理论的最少运行次数应该如下图，而不是这里的 $1/2(1-p)p$：

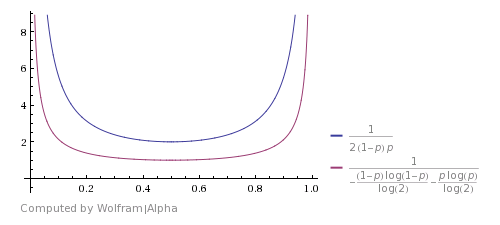
为什么会这样呢？因为这里只统计了 01 跟 10 这一对等概率事件，实际上有无穷对等概率事件存在，比如 0011 和 1100 等等。这么看确实是少统计了一些，自然就需要调用更多次才能出现想要的结果。

关于这个香农极限的计算详情可以看这个回答：Turn biased random number generator into uniform

最终解

回到我们的问题。运用上面的拒绝采样技术之后，我们终于可以得到一个在 $[0,N)$ 下的等概率随机器了。只不过我们的调用次数期望可能在 $floor(2^{32}/range)$ 和 $ceil(2^{32}/range)$ 之间。代码如下：

uint32_t random_bounded(uint32_t range) {
    uint64_t random32bit =  random32(); //32-bit random number 
    multiresult = random32bit * range;
    leftover = (uint32_t)multiresult;
    if (leftover < range ) {
        threshold = -range % range ;
        while (leftover < threshold) {
            random32bit =  random32();
            multiresult = random32bit * range;
            leftover = (uint32_t) multiresult;
        }
    }
    return multiresult >> 32;
}

看到上面那个调用次数的数学期望也不用太紧张。因为实际上 if 分支的进入次数并没有想象中那么多，几乎可以忽略不计。

作者最后也测试了一下几种不同语言的范围随机函数跟这两个版本的性能比较，结果如下：

Random shuffle timings, varying the range function
range function	cycles per input word
PCG library	18.0
Go-like	20.1
Java-like	12.1
no division, no bias	7
no division (with slight bias)	6

可以看到改造除法运算后，运行速度几乎是普通代码的 2 倍以上，效果还是相当明显的。

关于算法的详细分析，也可以参考一下 Daniel Lemire 的论文 Paper: Fast Random Integer Generation in an Interval。

参考：

Comments

programmer (22)

algorithm (15)