地牢随机
两年前,我们的策划想要一种随机迷宫的功能。当时策划想要的方案是由策划提供一些迷宫房间的模版,这些模版拥有不同的连通关系,也就是不同的开口方向,然后由程序根据这些房间的开口方向,按照策划的要求来随机生成连通的房间。
举例来说,比如策划给出一些房间模版如下:
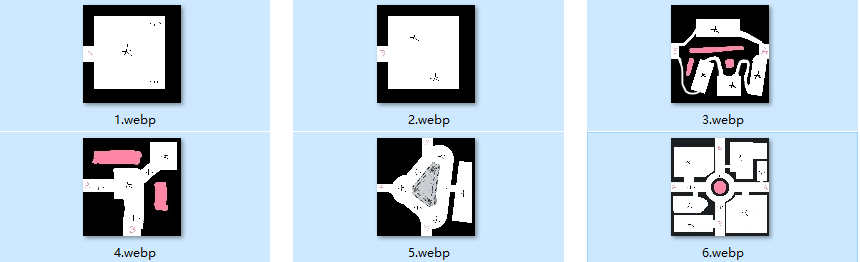
这些房间有 1 开口的出生房间、1 开口的终点房间、两种 2 开口的房间、一种 3 开口的房间、一种 4 开口的房间。通常地牢的出生房间跟终点房间会有不同的类型,虽然都是 1 开口连通的房间,这里也用两种不同的房间来表达。这样的 6 种不同连通关系的房间就涵盖了所有矩形房间的模式。相同的连通关系的房间可以设计出不同的内部细节,不过这属于策划的设计,不影响程序的随机逻辑。
策划希望能够指定迷宫的最大长宽以及房间的总数,并且指定起点跟终点房间的坐标。所以我写了这么一个库来做这件事情 maze_creator。算法比较暴力,就是通过固定的起点采用 BFS 的方式向周围遍历,寻找不同房间类型的组合能够满足房间长宽和数量的限制,如果失败则往上回溯。由于房间种类比较少,同时我们游戏需要生成的房间总数也比较少,虽然效率不高,但运行的还挺正常。
当然,我们的策划还有一些其他要求,例如策划并不希望最终生成的迷宫是一条直路,需要添加一些曲折的死胡同让玩家探索,所以在此基础上我又做了扩展房间的逻辑。最终生成这样一幅迷宫图:
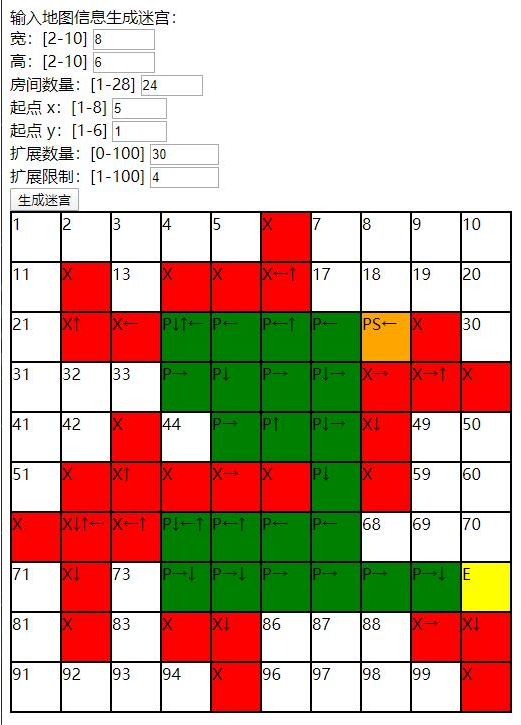
PS 表示起点、P 表示从起点到终点的最短路径、E 表示终点、X 表示扩展房间。每个房间里的箭头表示这个房间的开口方向。于是根据这样一幅图,把对应开口方向的房间替换进去就可以生成一个迷宫了。
比如我们正式游戏里的一个大关卡如下:
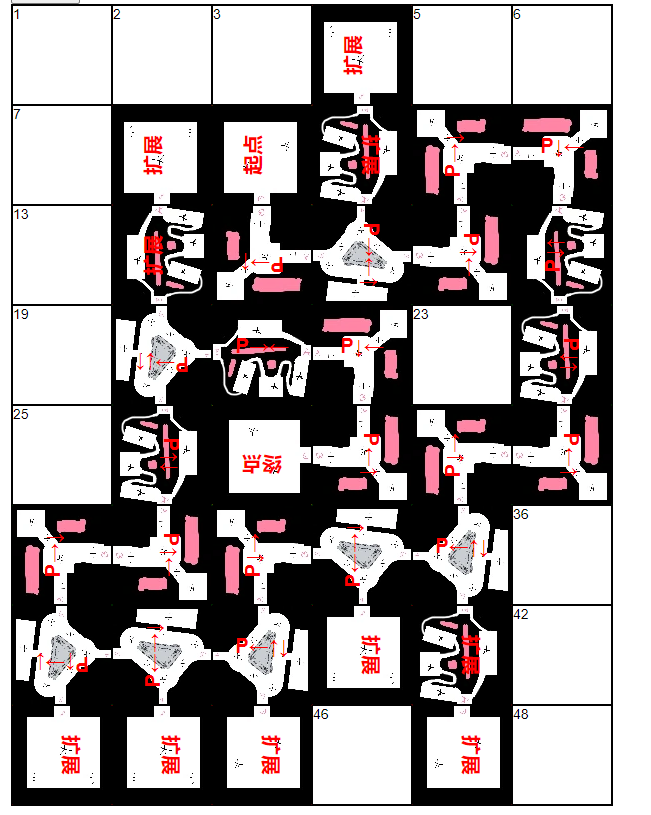
本来这件事就到此为止了。但最近我在玩《死亡细胞》的时候突然感兴趣起来,这种 roguelike 游戏的地牢是如何生成的呢?
D&D Dungeon Generator
于是我简单搜索了一下,发现了两种比较常见的靠谱 roguelike 随机地牢生成算法。其中一种是《龙与地下城》的迷宫生成算法,他们在网上做了一个迷宫生成器,非常的有意思,感兴趣的可以去试试:D&D Dungeon Generator。

这个算法的原理作者也在网上介绍了 Random Dungeon Design。我简单描述一下:
- 首先用路径填满一个指定地牢区域,这些路径能够形成一个从起点到终点的随机迷宫,其实这里生成迷宫的算法比较简单,比如用随机 BFS 填充即可
- 然后把生成的迷宫里那些岔路全部删掉,只保留下从起点到终点的唯一路径就好,当然在这种过程中如果去掉全部岔路可能导致迷宫被删掉的太多,所以可以设置删除长度,保留一部分的迷宫冗余
- 在剩余的迷宫路径上随机打孔,来把部分路径连起来,让迷宫看起来并不是那么唯一路径
- 在剩余的地牢区域随机出大小不一的房间,只要不覆盖到迷宫路径即可,然后把房间跟迷宫路径连起来
当然,从这个算法的过程看来,虽然没有那么明确,也就是步骤并不是固定的,尤其是最后摆放房间的过程,如果运气不好,随机的次数是不确定的。但是可以预估到大致是可以正常运行的,而且由于迷宫路径的设计可以复杂也可以简单,所以应该还是相当不错的。
当然,网上也有一些对这种方法的改进,比如这个 Rooms and Mazes: A Procedural Dungeon Generator。作者对《龙与地下城》的方法做了一些改进,针对的就是最后随机房间不确定的情况。改进的方式是先随机出不重叠的房间,然后在房间的空隙之间生成随机的小迷宫,然后通过洪泛算法随机选择一个房间,把迷宫跟房间之间通过开洞连接起来。最后去掉多余的迷宫路径就好。
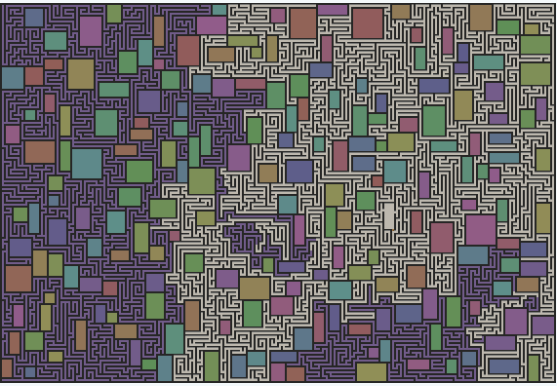
TinyKeep Dungeon Generation
另一种方式是《TinyKeep》游戏开发者在 reddit 上分享的方案 procedural_dungeon_generation_algorithm_explained。他的做法在我看来就要更确定一些了。简单描述如下:
- 首先在一个指定半径范围内生成若干随机长宽的矩形房间
- 然后通过 separation steering behavior 算法来把房间挪开,让他们相互不覆盖
- 然后挑选出一些长宽合理的房间作为地牢主房间
- 接着用 Delaunay Triangulation 算法来把所有主房间连接起来
- 接着通过 DT 图构造最小生成树,去掉 DT 图里不需要的边
- 为了乐趣,在 DT 图里随机出一些边添加回去。然后把不同的主房间用规则的直线或者折线连起来
- 为了地牢更加丰富,把靠近主房间同时被连线穿过的其他房间也包含进来
- 最后去掉所有其他不在包含内的房间就构造出了一个非常漂亮的迷宫

注意细节
这个算法中有好多细节需要注意:
一、圆内均匀取点:
比如第一步,如何在一个半径圆内随机出若干房间让他们分布均匀,其问题其实是如何在一个圆内随机点,让这些点满足均匀分布。一个常见的思路就是先随机一个 $[0,R)$ 的半径,然后随机一个 $[0, 2π)$ 的角度。但是这样最终得到的点的部分在整个圆的面积上并不均匀,而是更靠近圆心一些:
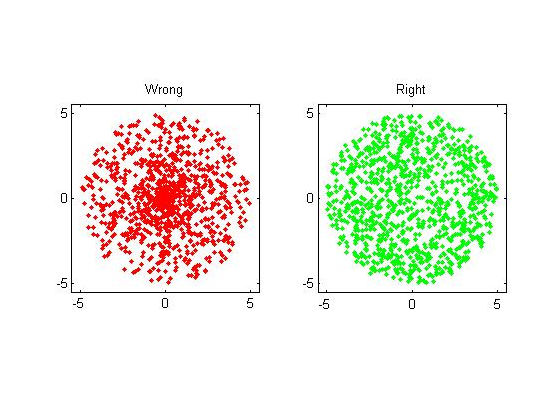
那么应该如何取点呢? 如果是极坐标可以这么取:
r = R * sqrt(random())
theta = random() * 2 * PI
如果是直角坐标可以这么取:
x = centerX + r * cos(theta)
y = centerY + r * sin(theta)
关于这部分可以查看这个问题的答案 Generate a random point within a circle (uniformly),或者更加一般性的解释在这里可以找到 在圆中均匀分布随机点。这里我就不做过多解释了。
二、separation 算法:
第二步通过 separation 算法来让房间相互隔开,这里的算法 separation steering behavior 其实是群体移动算法中的一个部分,关于群体移动一个比较有名的算法是 Boids,这个算法也是我之前研究群体逻辑的时候使用的一个算法。感兴趣的朋友可以仔细看看。
三、Delaunay Triangulation:
德劳内三角剖分是一个非常有用的算法。我一直认为我们本科的课程缺少了《计算几何》这门关键的课。德劳内三角剖分就是一种对平面上点集 P 的三角剖分,使得 P 中没有点严格处于剖分后任意一个三角形外接圆的内部。简单的说就是把点集用三角形连接起来,同时使得这些三角形都非常的匀称均衡。也就是使得小的角更大。关于德劳内三角剖分的数学内容,可以参看一下这里的解释 计算几何第五周:完美三角剖分。
同时,对于如何用代码实现 Delaunay Triangulation,可以参考 1989 年 Paul Bourke 的论文 Triangulate Efficient Triangulation Algorithm Suitable for Terrain Modelling。里面的代码非常简洁,值得学习。
在研究德劳内三角剖分的时候,我还发现有人把这个方法利用到图像的 Low Poly 化中了 三角剖分算法(delaunay),项目也非常有意思,地址如下:Polyer。

如果我的感觉没错,这个方法应该在更多的地方会产生应用。于是我又搜索了一下,发现原来在路由转发协议里,也使用了类似的方法来寻找最短的路径,当然,其使用的是德劳内三角剖分的一个更加小的子集 RNG 图 GPSR: Greedy Perimeter Stateless Routing for Wireless Networks
最后
等下次我再写地牢随机的时候想法就更多了,开心:D